演習課題1-15

二次元配列−3x3行列の和、差、積

問題

• 以下の機能を持つプログラムを、「プログラム作成の系統的な手順」に従って作成せよ。
  1. 指定された3x3の行列（行列1または行列2）に値を入力する
  2. 行列1+行列2を求めて行列3に入れる
  3. 行列1-行列2を求めて行列3に入れる
  4. 行列1ｘ行列2を求めて行列3に入れる
  5. 行列1、行列2、または行列3（計算結果を保持）を表示する
  6. 行列1ｘ行列2の中間式を表示する。なお、負の数は（）で囲むこと
  7. プログラムを終了する
• 5種類の機能を個別に実行できるようにすること
• 行列の要素はint型
• 行列の要素の初期値は0
• 行列の積C=AxBにおける計算式を以下に示す。

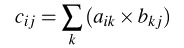
• 行列1ｘ行列2の中間式表示例を以下に示す。
  　1*(-1)+2*(-4)+3*(-7)    1*(-2)+2*(-5)+3*(-8)    1*(-3)+2*(-6)+3*(-9)
  　4*(-1)+5*(-4)+6*(-7)    4*(-2)+5*(-5)+6*(-8)    4*(-3)+5*(-6)+6*(-9)
  　7*(-1)+8*(-4)+9*(-7)    7*(-2)+8*(-5)+9*(-8)    7*(-3)+8*(-6)+9*(-9)

演習問題の考え方

• 関数
  • 主プログラム(main) 
  • 指定された行列を入力する（getMatrix）
  • 指定された行列を表示する（showMatrix）
  • 行列の和を求める（addMatrix）
  • 行列の差を求める（subtractMatrix）
  • 行列の積を求める（multiplyMatrix）
  • 行列の積の中間結果を表示する（showMultiplicationFormula）
  • 機能を一覧表示する（showMenu）

アルゴリズム

主プログラム

1. 機能を一覧表示する。

2. 機能番号を入力する。

3. 機能番号が「終了」でない限り以下の処理を繰り返す。

3-1. 機能番号が「行列の入力」ならば、以下の処理を実行する。

3-1-1. 行列番号(1=配列1 or 2=配列2)を入力する。

3-1-2. 指定された行列に値を入力する。

3-2. 機能番号が「行列の表示」ならば、以下の処理を実行する。

3-2-1. 行列番号（1=配列1, 2=配列2  or 3=計算結果）を入力する。

3-2-2. 指定された行列を表示する。

3-3. 機能番号が「行列の和」ならば、行列の和を求める。

3-4. 機能番号が「行列の差」ならば、行列の差を求める。

3-5. 機能番号が「行列の積」ならば、行列の積を求める。

3-6. 機能番号が「中間式の表示」ならば、行列の積を求める中間式を表示する。

3-7. 機能を一覧表示する。

3-8. 機能番号を入力する。

指定された行列に値を入力する

指定された行列を表示する

引数:指定された行列

アルゴリズムはプログラミング演習1-10を参考にすること。

行列の和を求める

引数:行列1、行列2、計算結果

1. 各行row に対して以下の処理を繰り返す

1-1. 当該行の各列column に対して以下の処理を繰り返す。

1-1-1. 行列1のrow行 column列の値と行列2のrow行 column列の値を加えて、計算結果のrow行 column列に代入する。

 

行列の差を求める 

引数:行列1、行列2、計算結果

1. 各行row に対して以下の処理を繰り返す

1-1. 当該行の各列column に対して以下の処理を繰り返す。

1-1-1. 行列1のrow行 column列の値から行列2のrow行 column列の値を引いて、計算結果のrow行 column列に代入する。

行列の積を求める

1. 各行row に対して以下の処理を繰り返す

1-1. 当該行の各列column に対して以下の処理を繰り返す。

1-1-1. 計算結果のrow行 column列を 0 とする。

1-1-2. 変数 iの値を0〜N-1まで変えながら以下の処理を繰り返す。

1-1-2-1. 行列1のrow行 i列の値と行列2のi行 column列の値を乗じて、計算結果のrow行 column列に加算する。

行列の積を求める中間式を表示する

1. 各行row に対して以下の処理を繰り返す。

1-1. 当該行の各列column に対して以下の処理を繰り返す。

1-1-1. 変数 iの値を0〜N-1まで変えながら以下の処理を繰り返す。

1-1-1-1. 行列1のrow行 i列の値を表示する。(負数の場合のみ()で囲む)

1-1-1-2. "*"を表示する。

1-1-1-3. 行列2のi行 column列の値を表示する。(負数の場合のみ()で囲む)

1-1-1-4. iがN-1でなければ"+"を表示する。

1-2. 改行する。

機能の一覧を表示する

プログラム

• Visual C++を使って、新しいプロジェクトenshu1_15を作る。
• matrixproduct.cppを追加し、アルゴリズムをプログラム化せよ。
• 入力したプログラムをコンパイルして、誤りを修正せよ。
• 修正が完了したプログラムを実行せよ。

レポート

• 提出物
  • ソースプログラム
• 提出期限：今週水曜日18:00
• 注意事項
  • プログラムを1つにまとめること
  • レポートの最終締め切りは定期試験前日とする。それまでに未提出分が無いかを確認して提出すること。

参考

• 2つの行列の入力と表示を行う。(課題はこれに演算を加えること）
• ベクトルの演算を行う。